Porque usar Distribuição Exponencial
Este é um post que também virou vídeo, você pode conferir aqui.
A razão de escrever este post foi o presente de natal antecipado que o Fábio Akita nos deu com seu vídeo “Média Salarial NÃO Existe - Entendendo Power Laws”. Mesmo não conhecendo o termo “Power Law”, como Akita linkou isso á distribuições de probabilidade, ficou fácil pegar o conceito. Até cheguei a comentar o vídeo tentando contribuir com meus 2 centavos, o que era para trazer maior clareza, aparentemente confundiu mais um pessoal.
Bom, Distribuições de probabilidade é um tema que vivi durante todos os meus longos 7 anos na faculdade. Sim, 7 anos. Já falei em outros post sobre isso, e da onde tirava minha motivação em terminar a faculdade.
Em Estatística, embora muita gente acredite que é apenas “tacar” a distribuição Normal e usar uma tabela de probabilidades prontas, na verdade estudamos diversas outras distribuições de probabilidade, como: Exponencial, t-student, Gama, Gama Generalizada, Exponencial Estendida, Exponencial Geométrica… enfim, o que mais tem é artigo criando distribuições de probabilidade nova para resolver algum problema específico, isso faz parte da pesquisa acadêmica na área. Sem contar as diferentes abordagens de inferência estatística, como máxima verossimilhança e inferência Bayesiana. Para falar a verdade tive uma iniciação científica na área de Análise de Confiabilidade realizando inferência bayesiana para distribuição Exponencial Geométrica Estendida. Olha que nome! Você nunca deve ter ouvido falar sobre essa distribuição de probabilidade.
O que devemos entender de importante aqui é: cada evento que observamos no mundo pode ser descrito a partir de um modelo probabilístico (em que na prática você desconhece, você não sabe que modelo é este). O que fazemos é coletar dados e ajustar diversos modelos (equações) diferentes e entender qual descreve melhor o comportamento observado. Logo, quanto mais modelos temos na literatura (e mais dados), maior a chance de modelarmos corretamente um evento de interesse.
Depois de ter feito essa paralela, podemos voltar ao vídeo do Akita. Logo que ele mostrou o case do Twitter, mesmo antes de apresentar os dados eu já estava imaginando que o comportamento seria de uma Distribuição Exponencial, justamente pelo tipo de comportamento do evento que seria modelado: contagem.
Esta é a vantagem de conhecer um pouco sobre as distribuições de probabilidade, sabendo suas propriedades você pode eliminar alguns modelos e assumir outros. Por exemplo, a cara da distribuição exponencial é essa:
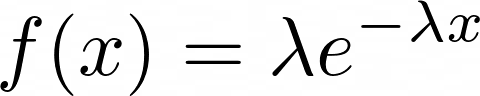
E ela pode ter alguns formatos diferentes dependendo do valor de lambda:
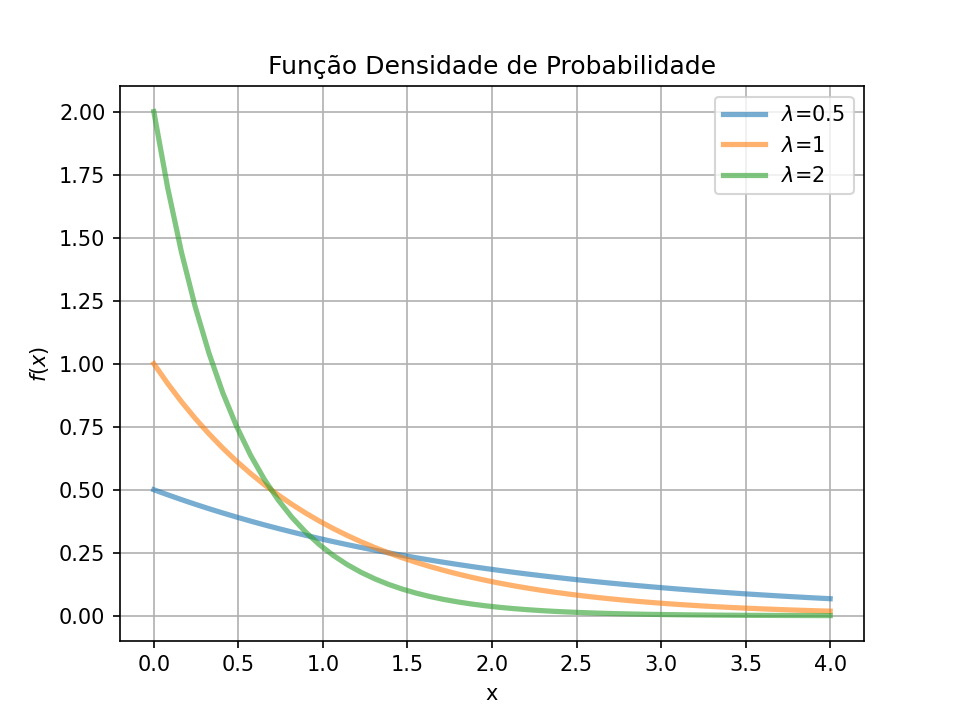
Agora uma parada importante! O x na função é seu evento (variável) de interesse e deve ser positivo. Quais exemplos temos que só podem ser positivos? Quantidade de seguidores? Salário? Tempo até ser curado de um câncer? Quantidade de amigos? Patrimônio? Tempo até conseguir primeiro emprego? Há uma grande chance da distribuição exponencial descrever bem estes dados. O que precisamos fazer é encontrar o melhor lambda para o conjunto de dados.
Aqui então temos a distribuição dos dados do Twitter…
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("../data/data.csv", sep=";")
plt.hist(df["follower"])
plt.xlabel("Quantidade de Seguidores (Milhões)")
plt.ylabel("Quantidade de Influenciadores")
plt.grid(True)
plt.title("Histograma para quantidade de seguidores")
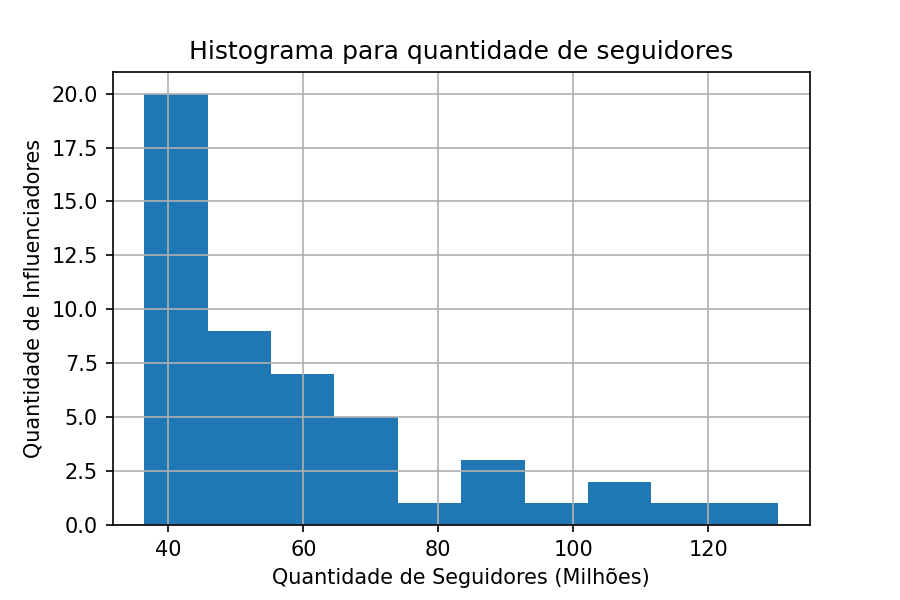
Repare como a distribuição dos dados é concentrada ao lado esquerdo, onde temos muitos influenciadores com baixos valores de seguidores. E são poucos os influenciadores com muitos seguidores. Agora, podemos ajusta o modelo Exponencial nestes dados, encontrando o melhor lambda.
from scipy.stats import expon
import numpy as np
pars_exp = expon.fit(df["follower"]) # Ajusta o modelo
dist_exp = expon(loc=pars_exp[0], scale=pars_exp[1]) # Define a distribuição com parâmetros encontrados
x_exp = np.linspace(dist_exp.ppf(0.01), dist_exp.ppf(0.99), 100) # Cria pontos para o modelo ajustado
plt.hist(df["follower"], density=True)
plt.plot(x_exp, dist_exp.pdf(x_exp), 'r-', lw=2.5, alpha=0.6)
plt.xlabel("Quantidade de Seguidores (Milhões)")
plt.ylabel("Quantidade de Influenciadores (densidade)")
plt.grid(True)
plt.title("Histograma para quantidade de seguidores")
plt.legend(["Modelo Exponencial Ajustado"])
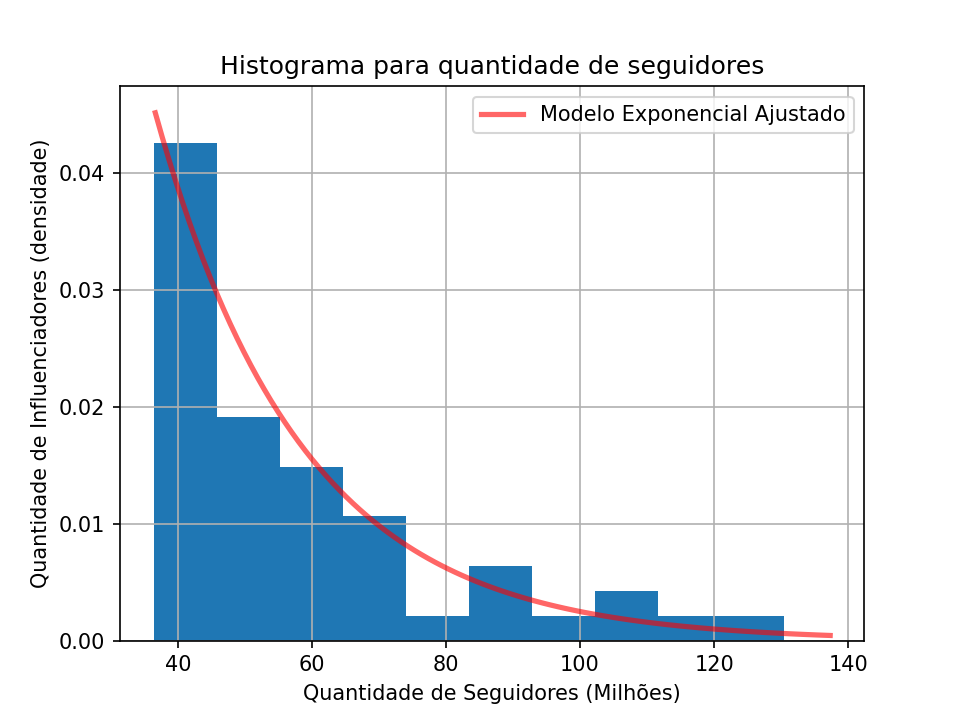
Agora sim temos a prova de que estes dados tem muito a cara de uma distribuição Exponencial. Mas vamos tentar ajustar uma Gaussina para ver o que acontece?
from scipy.stats import norm
pars_norm = norm.fit(df["follower"]) # Ajusta o modelo
dist_norm = norm(loc=pars_norm[0], scale=pars_norm[1]) # Define a distribuição com parâmetros encontrados
x_norm = np.linspace(dist_norm.ppf(0.01), dist_norm.ppf(0.99), 100) # Cria pontos para o modelo ajustado
plt.hist(df["follower"], density=True)
plt.plot(x_exp, dist_exp.pdf(x_exp), 'r-', lw=2.5, alpha=0.6)
plt.plot(x_norm, dist_norm.pdf(x_norm), 'g-', lw=2.5, alpha=0.6)
plt.xlabel("Quantidade de Seguidores (Milhões)")
plt.ylabel("Quantidade de Influenciadores (densidade)")
plt.grid(True)
plt.title("Histograma para quantidade de seguidores")
plt.legend(["Modelo Exponencial Ajustado", "Modelo Normal Ajustado"])
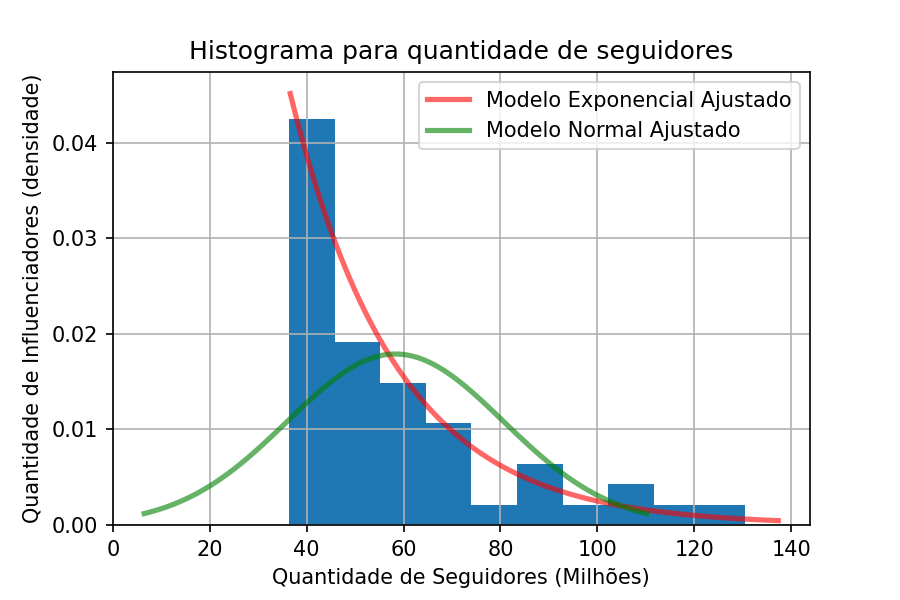
E ai, qual delas você escolheria para representar seus dados? Pois é, a distribuição Normal não faz sentido algum para estes dados. Assim, podemos descartá-la.
Gostaria então de agora trazer algumas propriedades desta distribuição que estamos falando tanto. A primeira delas, é algo que em todo bom material de probabilidade cita logo de cara. Que é a propriedade de falta de memória da distribuição exponencial, ou de um jeito mais elegante: propriedade Markoviana.
Em outras palavras, isso significa que caso um evento possa ser representado por uma distribuição Exponencial, o estado atual resume toda vida deste evento. Exemplo:
Se eu tenho 100 seguidores, é claro que já tive 99, 50, 10, 1 seguidor. Eu não preciso “carregar” essa informação, pois o número 100 já contêm essa informação em si próprio. A mesma ideia sobre pós graduação, para se ter este título, você teve que passar por ensino fundamental, médio, superior (via de regra). Então a informação do grau de instrução “resume” sua vida acadêmica.
Mais do que isso, em termos de probabilidade, é a mesma coisa ao dizer que um influenciador que tenha 1000 seguidores tem a mesma chance de chegar à 1500 seguidores do que um influenciado que tem 100 chegar à 600. Isto é, a probabilidade de ganhar 500 seguidores (em um espaço de tempo) independe da quantidade atual de seguidores. O que acaba dando a dinâmica de qual é o influenciador mais famosinho no momento, ou um influenciador que semana passada “não era ninguém” possa fazer tanto sucesso hoje.
Pensando da perspectiva de salário, que é realmente o tema do vídeo do Akita, este racional Markoviano é ainda mais interessante. Por exemplo, quando você recebe uma proposta de emprego, o que você considera ao te perguntarem a pretensão salarial? 10, 20, 30, 40% do seu salário atual? Importa se há um ano você ganhava metade disso ou mais? Ou ainda que na realidade acabou de ter um aumento? Assim, o seu salário atual resume bem a sua posição no mercado, e serve como (muitas vezes) ÚNICO balizador para uma nova posição.
Eu particularmente penso desta maneira: se a carreira é MINHA, então EU tenho que me posicionar no mercado com base no MEU salário atual em busca do próximo passo. Nem preciso dizer que com essa lógica não faz sentido algum olhar para “a média do mercado”, pois o que realmente vale é a minha posição.
Falando em média, vamos dar mais uma olhada na distribuição Exponencial. Se calcularmos a média dos dados, qual seria o valor?
avg = round(df["follower"].mean())
plt.hist(df["follower"], density=True)
plt.plot(x_exp, dist_exp.pdf(x_exp), 'r-', lw=2.5, alpha=0.6)
plt.vlines(avg, ymin=0, ymax=0.04, linestyles="--", colors="royalblue")
plt.xlabel("Quantidade de Seguidores (Milhões)")
plt.ylabel("Quantidade de Influenciadores (densidade)")
plt.grid(True)
plt.title("Histograma para quantidade de seguidores")
plt.legend(["Modelo Exponencial Ajustado", f"Média dos dados: {avg:.0f}"])
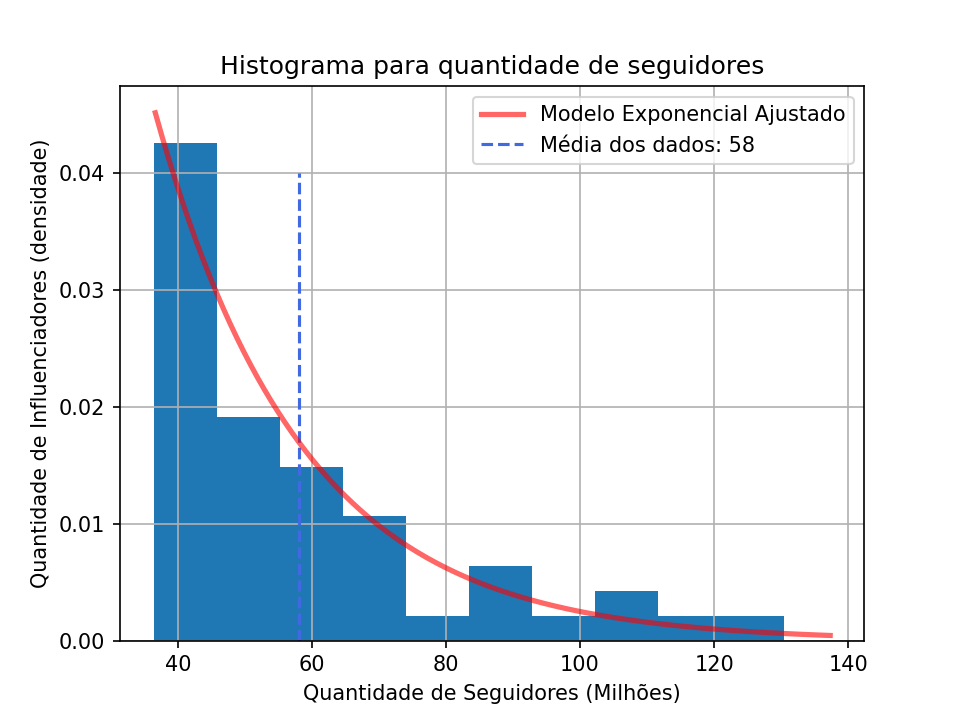
Você realmente acha que este valor resume de forma correta toda essa distribuição dos dados? Será que usando esta medida estamos inferindo a realidade do mercado? Para estes dados temos um comportamento assimétrico, onde a calda da direita acaba puxando a média para cima, ou seja, distorce a média para valores mais altos.
No tema de salário, isso acaba passando a mensagem de que os valores são mais altos do que realmente são. Mas então qual outra medida podemos usar? Mediana, talvez?
median = round(df["follower"].median())
plt.hist(df["follower"], density=True)
plt.plot(x_exp, dist_exp.pdf(x_exp), 'r-', lw=2.5, alpha=0.6)
plt.vlines(avg, ymin=0, ymax=0.04, linestyles="--", colors="royalblue")
plt.vlines(median, ymin=0, ymax=0.04, linestyles="--", colors="orange")
plt.xlabel("Quantidade de Seguidores (Milhões)")
plt.ylabel("Quantidade de Influenciadores (densidade)")
plt.grid(True)
plt.title("Histograma para quantidade de seguidores")
plt.legend(["Modelo Exponencial Ajustado",
f"Média dos dados: {avg:.0f}",
f"Mediana dos dados: {median:.0f}"])
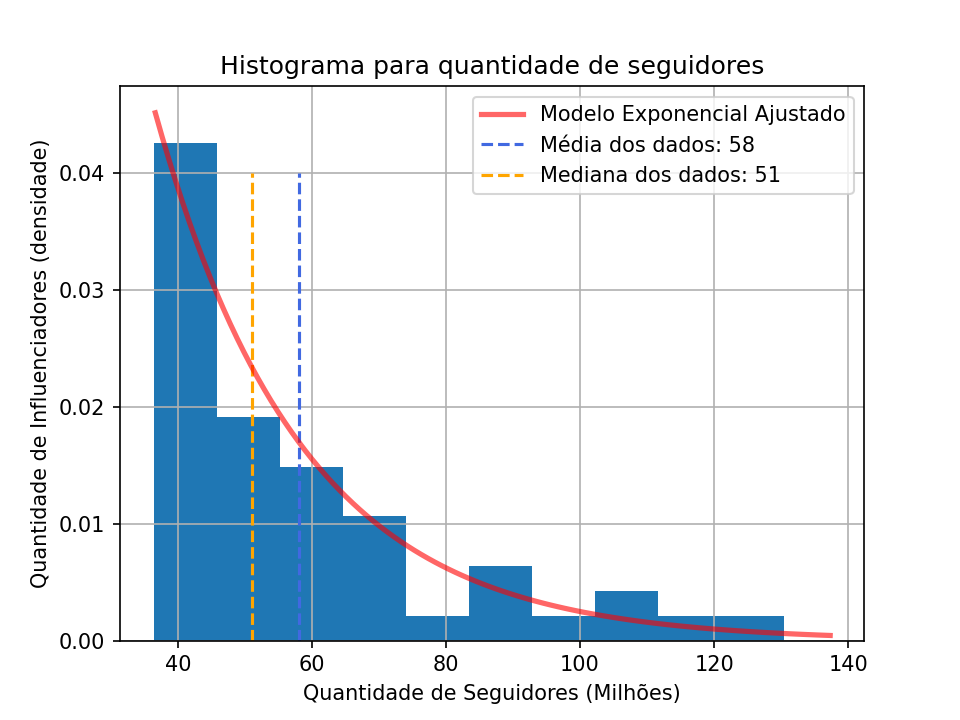
Ou seja, 50% dos influencers tem entre 36 e 51 Milhões de seguidores. Note como a outra metade tem uma dispersão muito maior, chegando até 130 milhões. Imagina como isso se comporta no mercado?
Não posso encerrar este post sem deixar duas provocações.
Considerando tudo o que vimos, se você pudesse ordenar todos os profissionais de sua área com base em nível de co nde salto em percentis na distribuição de salário. É como olhar para este gráfico e cada novo seguidor que um influenciador ganha, o joga mais e mais para cima nos percentis.
Por último, se você já está em um percentil alto (ou no que você acredita se suficiente para sua carreira), ajude outros a chegarem lá também. É isso que ajudará a termos uma sociedade menos desigual e com menos pobreza. Apesar do comportamento do mercado seguir uma distribuição onde a maioria é desfavorecida, podemos ao menos diminuir a escala (amplitude) dessa desigualdade, ainda que a forma da curva se mantenha, podemos torná-la mais estreita. Assim diminuímos a concentração de riqueza, i.e. distância entre mais rico e mais pobre diminui.
Para vocês terem uma ideia melhor sobre essa desigualdade, encerro este post com um link de calculadora do salário do brasileiro, onde você consegue identificar em qual percentil se encaixa:
https://www.bbc.com/portuguese/brasil-57909632